貝氏定理

貝氏定理
========

對一般人而言，「下雨、帶傘」的原則雖是大致相同，
但仍存在些個別差異。
一般來說，「下雨」是帶傘的【原因】之一，
而「帶傘」是下雨的可能【結果】。

對呂老師而言，每當下雨之時，他大多會帶著傘，
據其描述「每當下雨時，會帶傘應有 90% 的機會如此」。

然而，當不下雨的時候，他偶而也會帶傘，
有時是太陽太酷熱，遮陽之用，有時是充當手杖使用，
據其描述，「每當不下雨時，偶而也會帶傘的機會應有 20% 的機會如此」。

[Q1]
今天，在密閉的教室中，你看到呂老師從外面走進來，帶著傘，
請問：「外面下著雨」的機率為何？

[Ans1]: 傘 >> 雨 :  P(雨 | 傘) = .45 / .55 ~~ .82

  
(不)雨 >> (不)傘,    當(不)下雨時，(不)帶傘:

		傘	不傘
0.5	雨	0.9	0.1	1
0.5	不雨	0.2	0.8	1

(不)雨 且 (不)傘, 

		傘	不傘
	雨	0.45	0.05	0.5
	不雨	0.10	0.40	0.5
		0.55	0.45

(不)傘 >> (不)雨,    當(不)帶傘時，(不)下雨: 

		傘	不傘
		.45/.55	.05/.45	雨
		.10/.55	.40/.45	不雨
		1	1

[解說]: 

本來，沒有任何情報之下，
在密閉教室內猜測外面有沒有下著雨時，
我們認為，樣本空間 S = { '雨',  '不雨' }，
假設2個情形(樣本)的可能性相等，
又機率公設中， P(S)=1。

因此，P( '雨') = P( '不雨') = 1/2 = 0.5
現在，有了呂老師帶傘與下雨之間的情報之後，
又觀測到呂老師確實帶傘，
運用貝式定理後，重新估測下雨的機率，
其結果有所改變，
從 0.5 變成 .45 / .55 ~~ .82 了。

====

[Q2]
進一步，若你知道本教室位於林口地區，
一年之中，下雨的機率本就高於台灣其他地區，
據稱大約有 70% 的日子會下雨，
根據這項情報，請重新估測：
「外面下著雨」的機率為何？

[Ans2]: 傘 >> 雨 :  P(雨 | 傘) = .63 / .69 ~~ .91

(不)雨 >> (不)傘,    當(不)下雨時，(不)帶傘:

林口地區		傘	不傘
0.7	雨	0.9	0.1	1
0.3	不雨	0.2	0.8	1

 (不)雨 且 (不)傘, 

		傘	不傘
	雨	0.63	0.07	0.70
	不雨	0.06	0.24	0.30
		0.69	0.31

(不)傘 >> (不)雨,    當(不)帶傘時，(不)下雨:  

		傘	不傘
		.63/.69	.07/.31	雨
		.06/.69	.24/.31	不雨
		1	1

[解說]: 

完全沒有資訊，純猜測: P('雨')    = 0.5 

知道林口地區的下雨情報: P('雨') = 0.7

加上呂老師帶傘情報，並確實觀察帶傘這個事件，
根據貝是定理
P(雨 | 傘) = .63 / .69 ~~ .91



[Q3]
更進一步，若你知道本教室位於台灣的南部地區，
一年之中，下雨的機率似乎較低於台灣其他地區，
據稱大約僅有 40% 的日子會下雨，
根據這項情報，請重新估測：
「外面下著雨」的機率為何？


----

[Q4]
有位楊老師，她的習慣與呂老師不大一樣，
每當下雨之時，她有時雖也帶著傘，
但因為個性較為浪漫之故，
若是小雨，偶爾也會想要雨中漫步一番，
據其描述「每當下雨時，會帶傘應有 60% 的機會如此」。

根據這種情境，在 [Q1][Q2][Q3]的提到的地區裡，
在密閉的教室中，你看到楊老師從外面走進來，
【沒有】帶著傘，
請估測：
「外面【沒有】下雨」的機率為何？

----

Bayes' theorem

From Wikipedia, the free encyclopedia

In probability theory and applications, 

Bayes' theorem shows the relation between a conditional probability and its reverse form. 

For example, the probability of a hypothesis given some observed pieces of evidence 

and the probability of that evidence given the hypothesis. 

This theorem is named after Thomas Bayes 

and often called Bayes' law or Bayes' rule.

Formula

The equation used is:

Where:

• P(A) is the prior probability or marginal probability of A. 
• It is "prior" in the sense that it does not take into account any information about B.
• P(A|B) is the conditional probability of A, given B. 
• It is also called the posterior probability because it is derived from or depends upon the specified value of B.
• P(B|A) is the conditional probability of B given A. 
• It is also called the likelihood.
• P(B) is the prior or marginal probability of B. 
• It acts as a normalizing constant.

----

陳述

貝氏定理 是關於 隨機事件A和B的 條件機率的 一則定理。

其中P(A|B) 是在B發生的情況下 A發生的可能性。

在貝氏定理中，每個名詞都有約定俗成的名稱：

• P(A)是A的先驗機率或（或邊緣機率）。
• 之所以稱為"先驗"是因為它不考慮任何B方面的因素。
• P(A|B)是已知B發生後A的條件機率，
• 也由於得自B的取值而被稱作A的後驗機率。
• P(B|A)是已知A發生後B的條件機率，
• 也由於得自A的取值而被稱作B的後驗機率。
• P(B)是B的先驗機率或邊緣機率，
• 也作標准化常量（normalizing constant）。

按這些術語，貝氏定理可表述為：

後驗機率 = (相似度 * 先驗機率) / 標准化常量

也就是說，後驗機率 與先驗機率 和相似度的乘積 成正比。

另外，比例P(B|A) / P(B) 也有時被稱作標准相似度（standardized likelihood），

貝氏定理可表述為：

後驗機率 = 標准相似度 * 先驗機率

----

ベイズの定理（ベイズのていり、英: Bayes' theorem）とは、

条件付き 確率に 関して 成り立つ 定理で、

トーマス・ベイズに よって 示された。

なお ベイズ統計学に おいては 基礎として 利用され、

いくつかの 未観測要素を 含む推論等に 応用される。

----

概要

事象Aの ベイズ確率に ついて、

• P(A) = 事象Bが 起きる 前の、 事象Aの 確率
• （事前確率, prior probability）
• P(A|B) = 事象Bが 起きた 後での、事象Aの 確率
• （事後確率，条件付き確率, posterior probability，conditional probability）とする。 
• ベイズの定理を 使えば、事後確率 P(A|B) は 下記に 従って 計算される。
• 

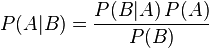
すなわち、事象Bに 関するある結果（データ）が 得られたとすると、 それを 反映し、尤度P(B|A) の 乗算によって、 事象Aの確率は 事前確率から 事後確率へと 更新される。なお 事象Aの 確率の 観点からは、P(B) は規格化定数としての 意味しかない。

ベイズ統計学（およびベイズ決定理論）は 上記の手続きに その基礎をおき、 名前の由来とも なっている。